Análisis de impedancia, impedancia de entrada e impedancia de salida

Impedancia es un término colectivo para resistencia y reactancia, y la mayor diferencia entre resistencia y reactancia es que la limitación de corriente de resistencia (ley de Ohm) consume energía eléctrica al mismo tiempo. La reactancia se limita a la corriente y no consume energía eléctrica (sin realizar trabajo). La resistencia tiene un efecto de corriente limitado tanto en corriente continua como en corriente alterna, mientras que la reactancia solo tiene un efecto de corriente limitado en entornos de corriente alterna.

La impedancia de entrada se refiere a la impedancia equivalente en el extremo de entrada de un circuito. Agregue una fuente de voltaje U al terminal de entrada y mida la corriente I en el terminal de entrada, luego la impedancia de entrada Rin es U/I. Puedes imaginar el extremo de entrada como los dos extremos de una resistencia, y el valor de resistencia de esta resistencia es la impedancia de entrada.

Bajo el mismo voltaje de entrada, si la impedancia de entrada es muy baja, es necesario que fluya una gran corriente, lo que prueba la capacidad de salida de corriente de la etapa anterior; Si la impedancia de entrada es alta, sólo se requiere una pequeña cantidad de corriente, lo que reduce una carga significativa sobre la capacidad de salida de corriente de la etapa frontal. Por lo tanto, en el diseño de circuitos, intente aumentar la impedancia de entrada tanto como sea posible.

La impedancia de entrada no es diferente de un componente de reactancia ordinario, ya que refleja la magnitud del efecto de bloqueo actual.

Para los circuitos controlados por voltaje, cuanto mayor sea la impedancia de entrada, más ligera será la carga en la fuente de voltaje, lo que facilitará el control sin afectar la fuente de señal; Para circuitos accionados por corriente, cuanto menor sea la impedancia de entrada, más ligera será la carga en la fuente de corriente.

Por lo tanto, podemos pensar que si se utiliza una fuente de voltaje para conducir, cuanto mayor sea la impedancia de entrada, mejor; Si es impulsado por una fuente de corriente, cuanto menor sea la impedancia, mejor (nota: solo apto para circuitos de baja frecuencia, en circuitos de alta frecuencia también se debe considerar la adaptación de impedancia). Además, al obtener la máxima potencia de salida, la impedancia También se debe considerar la coincidencia.Impedancia de salida

La impedancia de salida incluye la impedancia interna de la fuente de voltaje equivalente (circuito equivalente de Thevenin) o fuente de corriente equivalente (circuito equivalente de Norton) del puerto de salida de la red eléctrica independiente. Su valor es igual a la impedancia de entrada vista desde el puerto de salida cuando la fuente de alimentación independiente se establece en cero.

Independientemente de la fuente de señal, el amplificador y la fuente de alimentación, existe un problema con la impedancia de salida. La impedancia de salida es la resistencia interna de una fuente de señal. Originalmente, para una fuente de voltaje ideal (incluida la fuente de alimentación), la resistencia interna debería ser 0 o la impedancia de una fuente de corriente ideal debería ser infinita. La impedancia de salida necesita la mayor atención en el diseño de circuitos.

En realidad, las fuentes de voltaje no pueden lograr esto y una fuente de voltaje ideal a menudo se conecta en serie con una resistencia r para equivaler a una fuente de voltaje real. La resistencia r en serie con la fuente de voltaje ideal es la resistencia interna de la fuente de señal/salida del amplificador/fuente de alimentación.

Cuando esta fuente de voltaje suministra energía a la carga, una corriente I fluirá a través de la carga y generará I en esta resistencia × La caída de voltaje de r. Esto dará como resultado una disminución en el voltaje de salida de la fuente de alimentación, limitando así la potencia máxima de salida.

De manera similar, una fuente de corriente ideal debería tener una impedancia de salida infinita, pero los circuitos reales son imposibles.

La impedancia de salida se refiere a la impedancia equivalente del circuito cuando la carga del circuito se ve desde el puerto de salida del circuito en la dirección opuesta. De hecho, se refiere principalmente a la impedancia medida por la fuente de energía en el extremo de salida, comúnmente conocida como resistencia interna.

Análisis de pensamiento de impedancia de circuitos de conmutación

Como se muestra en la siguiente figura, V1 continúa entregando corriente a R1 y el circuito actual en la figura se muestra con la flecha verde. ¿Qué métodos tenemos si queremos controlar el flujo de corriente a R1?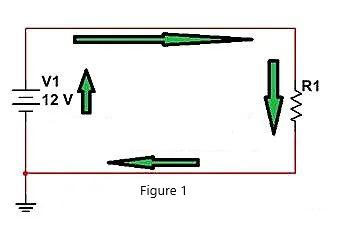

El método más común es desconectar la conexión entre V1 y R1 y cortar el circuito actual. Como se muestra en la siguiente figura.

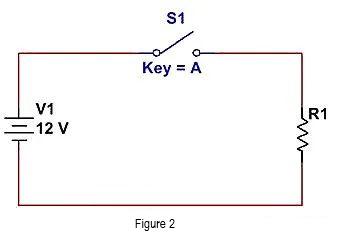
Alternativamente, podemos omitir R1 como se muestra en la siguiente figura. Agregue un cable delante de R1 para dirigir la corriente hacia el camino con baja impedancia, y R1 obtendrá una corriente insignificante.

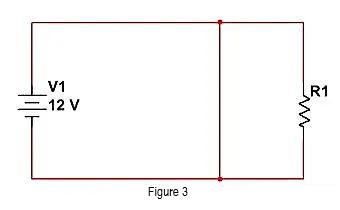
Los dos métodos anteriores son muy sencillos: desconectar completamente la ruta de V1 a R1 o cortocircuitar R1, lo que resuelve el problema por completo. Pero en el mundo de la ingeniería, no podemos hacerlo de manera tan limpia y ordenada, y a menudo enfatizamos un concepto "similar" en el mundo. acercarse. Entonces, en el "modelo de cortocircuito", solo podemos lograr "baja impedancia", mientras que en el "modelo de circuito abierto", solo podemos lograr "alta impedancia". Si la energía se "atenúa" significativamente, creemos que cumple con el estándar.

Como se muestra en la figura siguiente, se muestra el modelo de carga de energía real. Veamos cómo lograr el efecto de conmutación ajustando la impedancia. En los circuitos reales, las fuentes de energía tienen limitaciones de capacidad de salida y resistencia interna, y cuanto mayor es la corriente de salida, menor es el voltaje de salida.

El siguiente circuito tiene una resistencia interna de 0,1 Ω y una carga de 1 K Ω. En la situación actual, el voltaje obtenido en ambos extremos de la carga se compone de resistencia interna y voltaje parcial R2. Podemos calcular V=5V * (1K/(1K+0.1))=4.9999V, I=5V/1000.1 Ω=4.9mA.

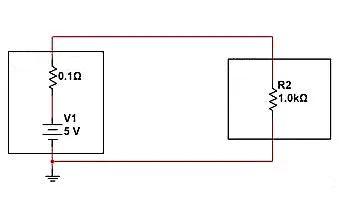
Si utilizamos el "modelo de circuito abierto" Método para romper el circuito, ¿cómo debemos ajustar la impedancia? Se trata de conectar una resistencia mucho mayor que 1K en serie entre la fuente de alimentación y la carga, y realizar una división de voltaje en serie para reducir el voltaje obtenido en R2. Como se muestra en la siguiente figura, si una resistencia de 1M está conectada en serie con el divisor de voltaje de carga. Podemos calcular la distribución de tensión final entre los dos extremos de la carga:

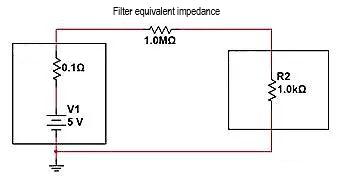
V=5V * (1K/(0,1+1000K+1K))=0,00499V, I=5V/1001000,1 Ω=0,0049mA. La amplitud se ha debilitado casi 1000 veces y, en el pensamiento de ingeniería, R2 está casi "desconectado".

Si utilizamos el "modelo de cortocircuito" Método para desconectar R2, ¿cómo debemos ajustarlo? Se trata de conectar una resistencia que es mucho menor que 0,1 Ω en paralelo en el extremo frontal de la carga y compartir el voltaje en serie con la resistencia interna, lo que da como resultado un voltaje más pequeño obtenido en R2.

Como se muestra en la siguiente figura, si la medida de filtrado es equivalente a una resistencia paralela de 0,005 Ω y un divisor de voltaje de resistencia interna. Podemos calcular la tensión final distribuida entre los dos extremos de la carga R2:

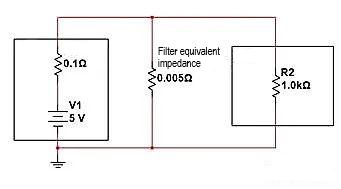
V = 5 V * (0,0049/(0,1 + 0,0049) = 0,233 V. La amplitud se ha debilitado casi 20 veces y, en el pensamiento de ingeniería, R2 también es similar a estar "desconectado".

Lo anterior es el modelo teórico de los circuitos de conmutación de semiconductores, tomando como ejemplo los circuitos inversores:

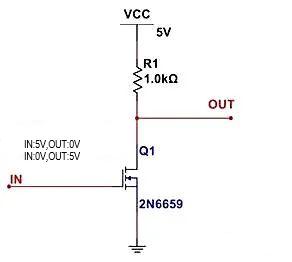
Cuando el extremo IN esté encendido, diremos que el transistor MOS Q1 está conduciendo. En este punto, el estado de conducción es equivalente a que Q1 se convierta en una resistencia con una impedancia de decenas de miliohmios y luego divida el voltaje con la resistencia R1. Si la resistencia pull-up R1 es demasiado pequeña y también tiene decenas de miliohmios, incluso si IN es alto y Q1 es conductor, el terminal OUT no puede generar un nivel bajo.

Cuando el extremo IN esté apagado diremos que el transistor MOS Q1 está cortado. En este punto, el estado de corte equivale a que Q1 se convierta en una resistencia con una impedancia de unos pocos megaohmios y divida el voltaje con la resistencia R1. Si la resistencia pull-up R1 es demasiado grande, que también es de unos pocos megaohmios, incluso si IN es bajo y Q1 está cortado, el terminal OUT no puede generar un nivel alto.

Entonces, para comprender profundamente los circuitos de conmutación, es necesario analizarlos con pensamiento de impedancia.

Circuito de filtro de análisis de pensamiento de impedancia

Aquí, analice el circuito de filtrado utilizando el pensamiento de impedancia.

En aplicaciones prácticas de ingeniería, una salida de energía a menudo contiene componentes de CA de diferentes frecuencias, tanto las que queremos como las que no queremos. La impedancia de la inductancia y la capacitancia variará con la frecuencia. Es precisamente por esta característica que los inductores y condensadores se han convertido en los actores principales de los circuitos de filtrado.

El siguiente circuito todavía se utiliza, asumiendo que la fuente de alimentación contiene un componente espectral de
0-1GHz.

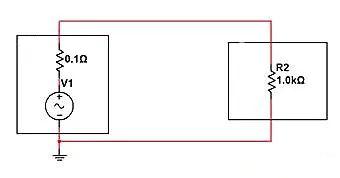
Si queremos filtrar los componentes de CA de alta frecuencia para la carga R2, encontraremos que tanto la inductancia en serie como la capacitancia en paralelo pueden cumplir los requisitos.
Como se muestra en la siguiente figura, si se conecta un inductor de 16 uH en serie entre la fuente de alimentación y la carga, ¿cuánto decaerá el componente de CA de 100 MHz? Según la fórmula de impedancia de la inductancia: ZL=2 π fL=2 * 3,14 * 100MHz * 16uH, se puede obtener ZL=10K.

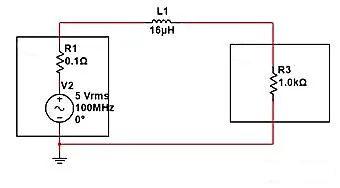
Según la fórmula del divisor de voltaje en serie, el voltaje/entrada en ambos extremos de R3=R3/(R3+ZL)=1K/11K=0.0909. Entonces, cuando la amplitud de la fuente de alimentación es de 5 V, la amplitud en ambos extremos de R3 es solo de 5 V * 0,0909 = 0,45 V.

A 100 MHz, utilice un osciloscopio para medir la forma de onda antes y después del filtrado. La comparación muestra que la forma de onda de 100MHz tiene un efecto y la medición real es 0.449V, lo que es consistente con los resultados del análisis.

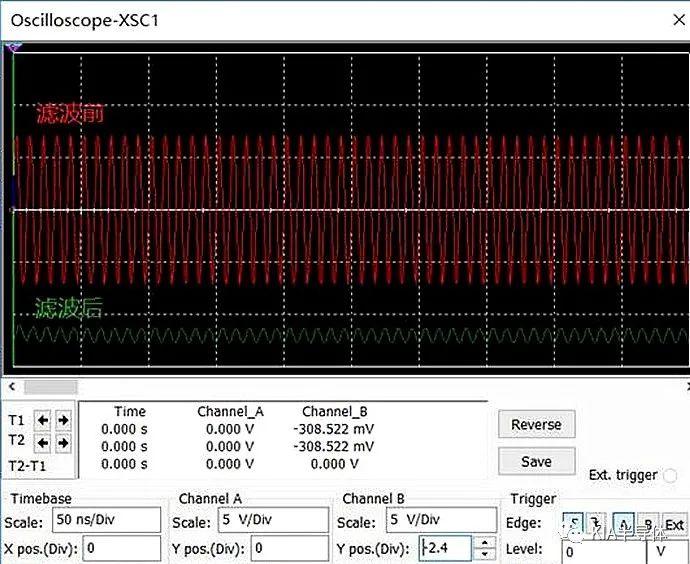
Análisis de pensamiento de impedancia de filtros de paso bajo.

Al conectar un inductor en serie entre la fuente de alimentación y la carga, y al conectar un capacitor en paralelo en el extremo frontal de la carga, se forma un circuito de filtro de paso bajo.

De la siguiente manera, si C1=1uF y L1=22uH, ¿cuál es el grado de atenuación del circuito de filtrado al
? ¿Componente de CA de 100 MHZ?

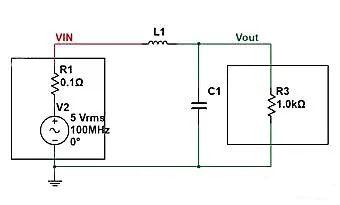
En este punto, el circuito se conecta en paralelo con la impedancia Zc del condensador (C1) y R3, y luego se divide con la impedancia ZL del inductor (L1). Entonces podemos enumerar la ecuación de impedancia (que es una fórmula simple del divisor de voltaje en serie).

Amplitud de atenuación=Vout/Vin=(Zc//R3)/(ZL+(Zc/R3)

Entre ellos, Zc=1/2 π fC y ZL=2 π fL. Dado R3=1K Ω, se puede concluir que Zc=0,0015 Ω, Zc/R=0,00149 Ω.

ZL=13816 Ω, la amplitud de atenuación se puede obtener como 0,00149/(13816,00149)=0,000000178.

Se puede ver que el componente de CA de 100 MHz difícilmente puede pasar a través del circuito de filtrado de paso bajo de 22 uH y 1 uF. Al mismo tiempo, también vemos que la carga R3 puede afectar el efecto de filtrado del filtro. Entonces, a veces nos encontramos con que el mismo circuito de filtro funciona bien en este circuito, pero mal en otros circuitos.